陶見の日記です
検索で画像リサイズのアルゴリズムで飛んでくる人が結構いるようなので、今回は画像縮小の定番「面積平均法」(別名:
(注.本見て調べたわけじゃないので間違い多いかも。ちなみにこの方法は画像を綺麗に縮小しようと考えると真っ先に考え付くものの1つかと思います。)
まずこの方式の特徴です。
・縮小向きです。拡大に使うのはお勧めしません。
・写真、イラストなど幅広く使え、自然な仕上がりになります。
・計算速度は結構速い。
・考え方がシンプルでわかりやすい。
では説明~といっても文で書くより、絵のが早いかと思いますので。

っと、以上です!(短っw)
ここでワンポイントアドバイス!
これ積で計算するので横と縦分けて計算しても結果一緒になるかと思います。
つまり初めに横方向だけ縮めて、さらにその画像を縦だけリサイズしても結果は同じというわけです。
もう一点、計算方法ですが分数(≒浮動小数点)を使わず整数だけでやる方法もあります。
では説明~といっても文で書くより、やっぱり絵のが早いかと思いますので。
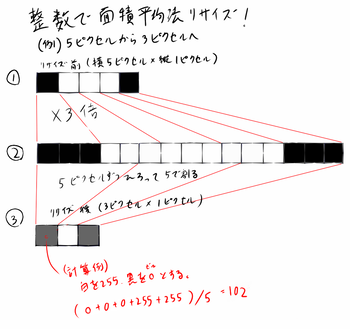
わかりました??・・・といってもこれあまりお勧めしません。常に2分の1とか3分の1とかに縮小なら早くていいのですが、たとえば1000ピクセルを999ピクセルに縮小とか考えてみてください・・・
まぁ、1000ピクセルを900ピクセルにリサイズなら②を900倍せずとも9倍して③で10ピクセルずつ拾ってやればいいのですが・・・要は縮小前と後のピクセル数の最小公倍数によって上図②がものすごい長くなる=計算量多くなっちゃうからです。
(面積平均法が縮小用な理由~)
面積平均法はドット1つ1つを四角と考えて面積比で色を混ぜてやる方法です。
そんなわけなので拡大に使うとドットがデッカイ四角となって拡大されるので無補完(ニアストレイバー法)と大して変わりません。移動や回転の補完についても四角が傾いたりして面積比出すのが面倒な上、線形補完と大して変わらない結果になるかと思われるので素直に線形補完使ったほうがいいかと思います。
====リサイズアルゴリズム関連記事====
・リサイズで色が濃くなる問題対策
・画像縮小アルゴリズム(とりあえずまとめっぽいもの)
・面積平均法の説明
(注.本見て調べたわけじゃないので間違い多いかも。ちなみにこの方法は画像を綺麗に縮小しようと考えると真っ先に考え付くものの1つかと思います。)
まずこの方式の特徴です。
・縮小向きです。拡大に使うのはお勧めしません。
・写真、イラストなど幅広く使え、自然な仕上がりになります。
・計算速度は結構速い。
・考え方がシンプルでわかりやすい。
では説明~といっても文で書くより、絵のが早いかと思いますので。
っと、以上です!(短っw)
ここでワンポイントアドバイス!
これ積で計算するので横と縦分けて計算しても結果一緒になるかと思います。
つまり初めに横方向だけ縮めて、さらにその画像を縦だけリサイズしても結果は同じというわけです。
もう一点、計算方法ですが分数(≒浮動小数点)を使わず整数だけでやる方法もあります。
では説明~といっても文で書くより、やっぱり絵のが早いかと思いますので。
わかりました??・・・といってもこれあまりお勧めしません。常に2分の1とか3分の1とかに縮小なら早くていいのですが、たとえば1000ピクセルを999ピクセルに縮小とか考えてみてください・・・
まぁ、1000ピクセルを900ピクセルにリサイズなら②を900倍せずとも9倍して③で10ピクセルずつ拾ってやればいいのですが・・・要は縮小前と後のピクセル数の最小公倍数によって上図②がものすごい長くなる=計算量多くなっちゃうからです。
(面積平均法が縮小用な理由~)
面積平均法はドット1つ1つを四角と考えて面積比で色を混ぜてやる方法です。
そんなわけなので拡大に使うとドットがデッカイ四角となって拡大されるので無補完(ニアストレイバー法)と大して変わりません。移動や回転の補完についても四角が傾いたりして面積比出すのが面倒な上、線形補完と大して変わらない結果になるかと思われるので素直に線形補完使ったほうがいいかと思います。
====リサイズアルゴリズム関連記事====
・リサイズで色が濃くなる問題対策
・画像縮小アルゴリズム(とりあえずまとめっぽいもの)
・面積平均法の説明
PR
Comment
